Center 2 1 Radius 4

Circle: Center-Radius Equation

A circumvolve is defined equally all the points (x, y) in a plane a fixed distance away from a stock-still heart point.

DEFINITION OF A CIRCLE:

All the points (x, y) in a plane that are equidistant from a fixed center betoken.

Figure 1 is a circle with the center , radius , and diameter identified.

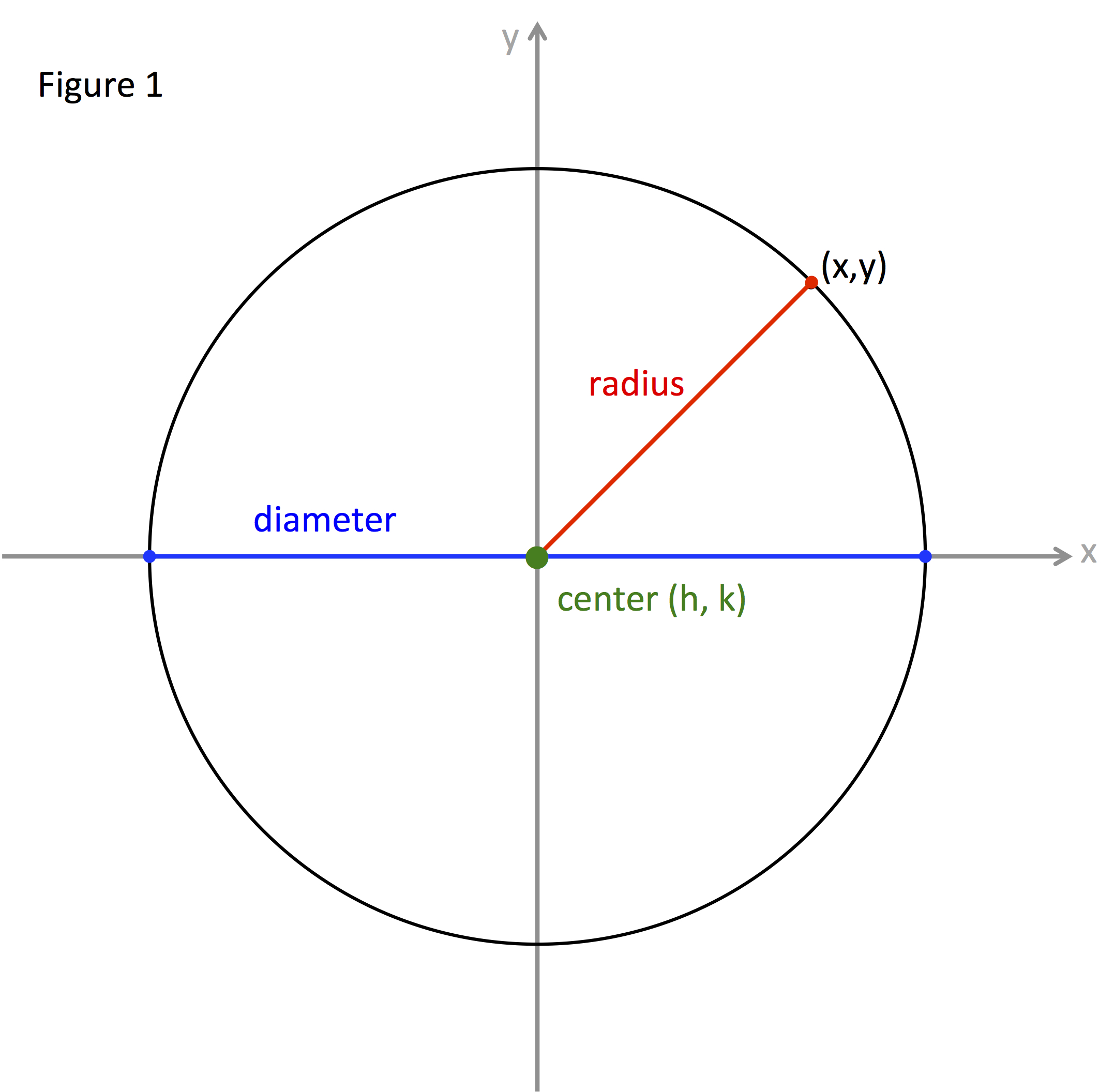
The center is a fixed point in the centre of the circle; usually given the full general coordinates (h, one thousand).

The fixed distance from the center to any indicate on the circle is called the radius .

A line segment from one signal on the circumvolve to another betoken on the circle that passes through the center is twice the radius in length. This line segment is called the diameter of the circle.

A circle tin be represented past 2 different forms of equations, the general grade and the centre-radius grade. This give-and-take will focus on the center-radius form.

Middle-RADIUS EQUATION:

Let the center be (h, k) and the radius be r.

${\left(x-h\right)}^2+{\left(y-k\right)}^2=r^2$

Let's apply the center-radius equation in some examples:

Example 1: What is the eye-radius equation of the circle with a diameter of 12 and a center at (-2, 5)

Step 1: Place the centre coordinates and the radius. The middle coordinates are given in the trouble. The radius must be determined from the bore, which is 2 times the radius or $r=\frac{d}{2}$.	Center: (-two, 5) Given $Radius=\frac{diamet\mathrm{eastward}r}{\mathrm{ii}}$ $r=\frac{12}{2}\to r=\mathrm{six}$
Step 2: Substitute the eye coordinates and radius into the centre-radius form. Be careful to include negative signs when substituting the center coordinates.	${\left(x-h\right)}^2+{\left(y-k\right)}^2=r^2$   Original ${\left[\mathrm{10}-\left(-2\right)\right]}^2+{\left(y-\mathrm{v}\right)}^2={\mathrm{half-dozen}}^2$ Sub. ${\left(x+\mathrm{two}\right)}^2+{\left(y-5\right)}^2=36$ Simplify

Case two: Circumvolve G has a radius of 8 and center at the origin. What is the positive x-coordinate of the point on the circle with a y-coordinate of -3?

Footstep i: Write the center-radius equation for the circle.	Heart: (0, 0) Given Radius = 8  Given ${\left(x-h\right)}^2+{\left(y-\mathrm{1000}\right)}^2=r^2$ Original ${\left(x-0\right)}^{\mathrm{two}}+{\left(y-0\right)}^2=8^{\mathrm{two}}$ Sub. ${\mathrm{ten}}^2+y^2=64$ Simplify
Step ii: Determine the 10-coordinate associated with a y-coordinate of -3. Substitute -3 in for y and solve for x.	$x^2+y^{\mathrm{two}}=64$ Original ${\mathrm{10}}^2+{\left(-\mathrm{three}\right)}^2=64$ Sub. $x^2+\mathrm{nine}=64$   Square $x^2=55$      Subtract $x=\sqrt{55}\approx 7.4$   Square Root

Center 2 1 Radius 4,

Source: https://www.softschools.com/math/pre_calculus/circle_center_radius_equation/

Posted by: torranceherrinfold.blogspot.com

Share this post